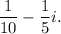Question

Find the quotient. Show all work for full credit.-2+i/-8-6i

Answer 1

=−2+-49/8i

Explanation:

-2+-49/8i

Answer 2

Answer: The required simplified quotient is
`(1)/(10)-(1)/(5)i.`

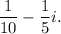
Step-by-step explanation: We are given to find the following quotient :

`Q=(-2+i)/(-8-6i)=(2-i)/(8+6i).`

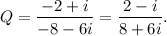
To find the given quotient, we must multiply both the numerator and denominator by the conjugate of (8+6i), that is, (8-6i).

So, we have

`Q\\\\\\=(2-i)/(8+6i)\\\\\\=((2-i)(8-6i))/((8+6i)(8-6i))\\\\\\=(16-12i-8i+6i^2)/(64-36i^2)\\\\\\=(16-20i-6)/(64+36)~~~~~~~~~~~~~~~~~~[\textup{since }i^2=-1]\\\\\\=(10-20i)/(100)\\\\\\=(1-2i)/(10)\\\\\\=(1)/(10)-(1)/(5)i.`

Thus, the required simplified quotient is
`(1)/(10)-(1)/(5)i.`