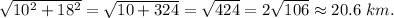Question

Caroline is geocaching in the woods, she walks 13 km due east, then 18 km north, finally 3 km west to find the cache.

What is the component form of the vector containing her final destination?
If Caroline’s friend travels the shortest root to the cache, how far will she walk?

Answer 1

`\vec{a}=(10,18).`

`2√(106)\approx20.6\ km.`

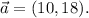
Explanation:

Let the initial Caroline's location be at the origin (0,0) and the directions be:

• north - positive y-direction;
• south - negative y-direction;
• east - positive x-direction;
• west - negative x-direction.

1. Caroline walks 13 km due east, then her location is (13,0).

2. Caroline walks 18 km to the north, then her location is (13,18).

3. Caroline walks 3 km west, then her location is (10,18).

Thus, the component form of the vector containing her final destination is

`\vec{a}=(10,18).`

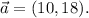
If Caroline’s friend travels the shortest root to the cache, she will walk

`√(10^2+18^2)=√(10+324)=√(424)=2√(106)\approx20.6\ km.`