Question

Given: △ABC, BK=10, AC=30,

m∠NMO=90°,
MN=MO, BK⊥AC, NO ∥AC, M∈AC
Find: NO

Answer 1

12 units is NO

Explanation:

Answer 2

12 units.

Explanation:

Consider right triangle MNO. This triangle is isosceles triangle, because MN = MO. Let NO = 2x units. NO is the hypotenuse in right triangle MNO, then MD = x units (the height in isosceles triangle is also its median and the median drawn to the hypotenuse in the right triangle is half of the hypotenuse).

Triangles NBO and ABC are similar triangles, then

`(NO)/(AC)=(h)/(BK),`

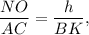
where h is the height of the triangle NBO.

Since BK =10 units and MD = x units, the height h = 10 - x units.

Thus,

`(2x)/(30)=(10-x)/(10),\\ \\20x=30(10-x),\\ \\20x=300-30x,\\ \\50x=300,\\ \\x=6\ un.`

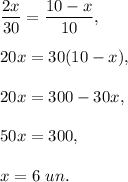
Hence, NO = 12 units.