Answer:
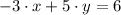 ,
,
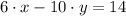 is inconsistent.
is inconsistent.
Explanation:
Two linear equations are inconsistent when each group of coefficients associated with each variable have the same multiple and independent coefficients are different and have the same multiple. Since, the set of variables is
 , then the following condition must be observed:
, then the following condition must be observed:
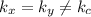 (1)
(1)
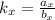 (2)
(2)
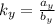 (3)
(3)
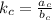 (4)
(4)
Now we proceed to check each option:
Option 1:
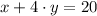 ,
,
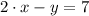
(
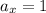 ,
,
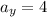 ,
,
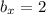 ,
,
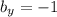 )
)
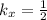 ,
,
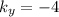 (This system is not inconsistent)
(This system is not inconsistent)
Option 2:
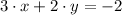 ,
,
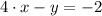
(
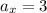 ,
,
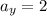 ,
,
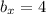 ,
,
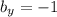 )
)
 ,
,
 (This system is not inconsistent)
(This system is not inconsistent)
Option 3:
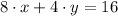 ,
,
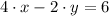
(
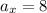 ,
,
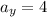 ,
,
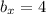 ,
,
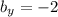 )
)
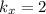 ,
,
 (This system is not inconsistent)
(This system is not inconsistent)
Option 4:
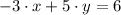 ,
,
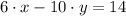
(
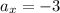 ,
,
 ,
,
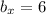 ,
,
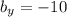 )
)
 ,
,
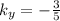 (This system may be inconsistent)
(This system may be inconsistent)
(
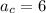 ,
,
 )
)
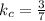 (This system is inconsistent)
(This system is inconsistent)