Question

From the roof of a building, a ball is thrown into the air. The height of the ball, h, in

metres after t seconds is given byh = -t2 + 4t + 12.
a) What is the height of the building?
b) How long will it take for the ball to hit the ground?
c) What is the maximum height of the ball and when does it occur?
d) When will the ball have a height of exactly 7m above the ground?

Answer 1

a) The height of the building is 12 metres.

b) The ball will take 6 seconds to hit the ground.

c) The maximum height of the ball is 16 metres and occurs 2 seconds after launch.

d) The ball have a height of 7 meters above the ground 5 seconds after launch.

Explanation:

a) The roof of the building is represented by the initial height of the ball according to the function. If we know that
`t = 0\,s`, the height of the building, measured in metres, is:

`y = -(0\,s)^(2)+4\cdot (0\,s) + 12`

`y = 12\,m`

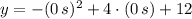
The height of the building is 12 metres.

b) Let equalise the given polynomial and solve for
`t` to determine the time taken for the ball to hit the ground:

`-t^(2)+4\cdot t +12 = 0` (1)

By the Quadratic Formula, we find the following solutions:

`t_(1) = 6\,s` and
`t_(2) = -2\,s`

Since time is a positive variable, then the only solution that is physically reasonable is:

`t = 6\,s`

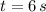
The ball will take 6 seconds to hit the ground.

c) The maximum height of the ball occurs when speed is equal to zero. First, we differentiate the function and equalise to zero:

`-2\cdot t + 4 = 0` (2)

`t = 2\,s`

Lastly, we evaluate the function at given time:

`y = -(2\,s)^(2)+4\cdot (2\,s)+12`

`y = 16\,m`

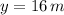
The maximum height of the ball is 16 metres and occurs 2 seconds after launch.

d) We equalise the height formula to seven and solve the resulting polynomial:

`-t^(2)+4\cdot t + 12 = 7`

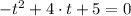`-t^(2)+4\cdot t +5 = 0` (3)

By the Quadratic Formula, we get the following solutions:

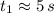`t_(1) \approx 5\,s` and
`t_(2) \approx -1\,s`

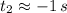
The only solution that is physically reasonable is
`t = 5\,s`.

The ball have a height of 7 meters above the ground 5 seconds after launch.