Question

Which of the following are solutions to the equation below 3x^2+27x=30

Answer 1

B.1 cause u can just use photo math

Answer 2

A. -10

B. 1

Explanation:

We are asked to find the solutions of the equations
`3x^2+27x=30`.

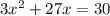Let us divide our equation by 3.

`(3x^2)/(3)+(27x)/(3)-(30)/(3)=0`

`x^2+9x-10=0`

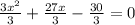
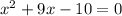
Let us factor out our equation by splitting the middle term. We need to figure out two numbers such that they add up-to 9 and their product should be -10.

We can see that 10 and -1 are these numbers as they add up-to 9 and their product is -10.

`x^2+10x-x-10=0`

`x(x+10)-1(x+10)=0`

`(x+10)(x-1)=0`

`(x+10)=0\text{ or }(x-1)=0`

`x+10-10=0-10\text{ or }x-1+1=0+1`

`x=-10\text{ or }x=1`

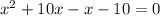
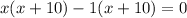
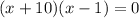
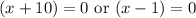
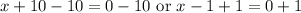
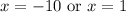
Therefore, -10 and 1 are solutions to our given quadratic equation and options A and B are correct choices.

We can also verify our answer by substituting our given values in the equation.

Let us check our given options one by one by substituting them in our equation.

A. -10

`3(-10)^2+27(-10)=30`

`3*100-270=30`

`300-270=30`

`30=30`

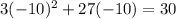
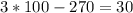
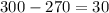
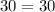
As both sides of our equation are equal, therefore, option A is the correct choice.

B. 1

`3(1)^2+27(1)=30`

`3*1+27=30`

`3+27=30`

`30+27x-30=0`

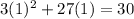
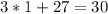
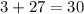
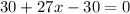
As both sides of our equation are equal, therefore, option B is the correct choice.

C. -1

`3(-1)^2+27(-1)=30`

`3*1-27=30`

`3-27=30`

`-24\\eq 30`

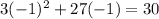
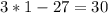
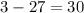
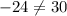
As both sides of our equation are not equal, therefore, option C is not a correct choice.

D. 10

`3(10)^2+27(10)=30`

`3*100+270=30`

`300+270=30`

`570\\eq 30`

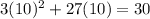
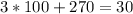
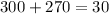
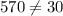
As both sides of our equation are not equal, therefore, option D is not a correct choice.

E. -2

`3(-2)^2+27(-2)=30`

`3*4-54=30`

`12-54=30`

`-42\\eq 30`

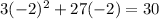
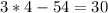
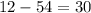
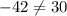
As both sides of our equation are not equal, therefore, option E and F are not correct choices as well.