Question

See attached files, Trigonometry

Answer 1

1) What is equivalent to
`(cos(x))/(1 + sin(x))`?

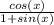Multiply the numerator and denominator by 1 - sin(x):

`(cos(x))/(1 + sin(x))` *
`(1 - sin(x))/(1 - sin(x))`

`(cos(x)(1 - sin(x)))/(1 - sin^(2)(x))`

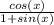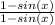
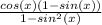
Use this trigonometric identity

cos²(x) + sin²(x) = 1

1 - sin²(x) = cos²(x)

Substitute this into the expression

`(cos(x)(1 - sin(x)))/(cos²(x))`

`(cos(x))/(1+sin(x))` =
`(1 - sin(x))/(cos(x))`

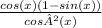
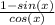
(first choice)

2) What is equivalent to 1 + cot⁴x?

Use this trigonometric identity

cos²(x) + sin²(x) = 1

Divide both sides by sin²(x)

cot²(x) + 1 = csc²(x)

1 = csc²(x) - cot²(x)

Multiply both sides by csc²(x) + cot²(x)

csc²(x) + cot²(x) = csc⁴(x) - cot⁴(x)

cot⁴(x) = csc⁴(x) - csc²(x) - cot²(x)

Add 1 to both sides

1 + cot⁴(x) = 1 + csc⁴(x) - csc²(x) - cot²(x)

Let's return to cot²(x) + 1 = csc²(x)

Multiply both sides by -1

-cot²(x) - 1 = -csc²(x)

-csc²(x) - cot²(x) = -2cot²(x) - 1

Substitute this into 1 + cot⁴(x) = 1 + csc⁴(x) - csc²(x) - cot²(x)

1 + cot⁴(x) = 1 + csc⁴(x) - 2cot²(x) - 1

1 + cot⁴(x) = csc⁴(x) - 2cot²(x)

(third choice)