Answer:
606 customers arrive at the counter over the 60 minute period.
Step-by-step explanation:
Given : The rate at which customers arrive at a counter to be served is modeled by the function F defined by
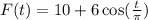
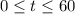 where F(t) is measured in customers per minute and t is measured in minutes.
where F(t) is measured in customers per minute and t is measured in minutes.
To find : How many customers arrive at the counter over the 60-minute period?
Solution :
We are going to integrate the function in the interval
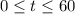 with respect to time.
with respect to time.
Function
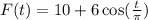
Integrate w.r.t t in the interval
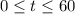
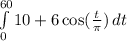
![=[10t+6\pi\sin((t)/(\pi))}]^(60)_(0)](https://img.qammunity.org/2020/formulas/mathematics/high-school/xv2boefdk8df4lcmoswl1ld4kmq8m6dcwf.png)
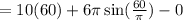
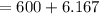
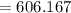
Approximately, 606 customers arrive at the counter over the 60 minute period.