Question

A person travels by car from one city to another with different constant speeds between pairs of cities. She drives for 10.0 min at 75.0 km/h, 6.0 min at 95.0 km/h, and 45.0 min at 40.0 km/h and spends 40.0 min eating lunch and buying gas.(a) Determine the average speed for the trip.

(b) Determine the distance between the initial and final cities along the route.

Answer 1

a) v = 0.515 km / min , b) x_total = 52 km

Step-by-step explanation:

The measured speed is defined by the distance traveled between the time

v =
`(\Delta x)/(\Delta t)`

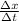
In this case they give us the speed in several time intervals

let's find the distance traveled in each interval

a) Goes at 75 km/h for 10 min

v =
`(x)/(t)`x / t

x₁ = v t

let's reduce speed to km / min

v₁ = 75 km / h (1h / 60 min) = 1.25 km / min

the distance traveled in this time is

x₁ = 1.25 10

x₁ = 12.5 km

b) goes to v = 95 km / h for 6 min

v = 95 km / h (1h 60 min) = 1.5833 km / min

the distance traveled is

x₂ = v₂2 t

x₂ = 1.58333 6

x₂ = 9.5 km

c) goes to v = 40 km / h for 45.0 min

v₃ = 40 km / h (1 h / 60min) = 0.6667 km / min

x₃ = 0.6667 45

x₃ = 30 km

d) t = 40 min, stopped

x₄ = 0

A) let's calculate the average speed of the trip

v =
`(x_(1)+x_(2)+x_(3)+x_(4) )/(t_(1)+t_(2)+t_(3)+t_(4) )`

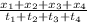
v = (12.5 +9.5 +30 +0) / (10 +6 +45 +40)

v = 52/101

v = 0.515 km / min

B) the distance between the two cities is

x_total = x₁ + x₂ + x₃

x_total = 12.5 +9.5 + 30

x_total = 52 km