Question

Write the linear inequality shown in the graph. The gray area represents the shaded region.

Answer 1

find it like a regular equation. find your slope and y intercept.

y ---- 4x - 2

since the shaded area is on the right and the coefficient is positive it most likely is less than. since the line is dashed it does not include the number (sign will be < or > without the or equal to)

so let's try it

y < 4x - 2

0 < - 2?

no

so shade on opposite side of the line

the answer is correct.

Answer 2

y < 4x - 2 is the inequality.

Explanation:

In this question we will find the equation of the given line first.

This line passes through two points (0.5, 0) and (0, -2).

So the slope of this line will be =
`(y-y')/(x-x')`

slope =
`(0+2)/(0.5-0)`

=
`(2)/(0.5)=4`

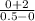
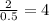
Y-intercept of the given dotted line is (-2)

Equation of the line will be y = 4x - 2

Now this line is in the dotted form so there is no equality, means it's a pure inequality.

So inequality may be y < 4x - 2 or y > 4x - 2

Now we will check the shaded area is for y < 4x - 2 or y > 4x - 2

Since gray area is on the right side of the inequality so we will take a point (2, 0) to check the inequality drawn on the graph.

0 < 4.(2) - 2

0 < 8 - 2

0 < 6 which is true.

For second inequality y > 4x - 2

0 > 4.(2) - 2

0 > 8 -2

0 > 6 which is not true.

Therefore, inequality representing the shaded area is y < 4x - 2