Question

Find the length to the nearest centimeter of the diagonal of a square 30 cm. on a side

Answer 1

42 cm.

Explanation:

Please find the attachment.

Let x be the length of diagonal of the square.

We have been given that length of each side of a square is 30 cm. We are asked to find the length of the diagonal of square to the nearest centimeter.

We can see from our diagram that triangle AC is the diagonal of our square.

Since all the interior angles of a square are right angles or equal to 90 degrees, so we will use Pythagoras theorem to find the length of diagonal.

`AC^2=AD^2+DC^2`

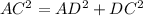
Upon substituting our given values in above formula we will get,

`x^2=(30\text{ cm})^2+(30\text{ cm})^2`

`x^2=900\text{ cm}^2+900\text{ cm}^2`

`x^2=1800\text{ cm}^2`

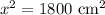
Let us take square root of both sides of our equation.

`x=\sqrt{1800\text{ cm}^2}`

`x=42.4264\text{ cm}\approx 42\text{ cm}`

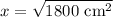
Therefore, the length of diagonal of our given square is 42 cm.