Answer: The answer is 4 and 32.
Step-by-step explanation: Let "A", "B" and "C" represents the set of students who were taking Arabic, Bulgarian and Chinese respectively.
The, according to the given information, we have

Let 'p' represents the number of students who take all the three languages, then
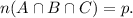
Also,
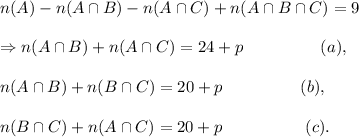
From here, we get after subtracting equation(c) from (b) that
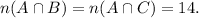
Therefore,
 and from equation (a), we find
and from equation (a), we find
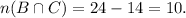
Thus,
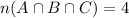 and
and
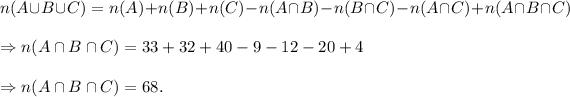
Thus, the number of students who take all the three languages is 4 and the number of students who take none of the languages is 100-68 = 32.