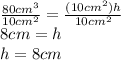Question

The volume of this pyramid is 80 cm cubed. What is its height? Triangular pyramid that has a right angle in the base, the sides adjacent of the right angle measure five centimeters and twelve centimeters, and the hypotenuse of the base is thirteen centimeters Question 7 options: 2.7 cm 4 cm 8 cm 13 cm

Answer 1

Third option: 8 cm

Explanation:

Volume of the pyramid: V=80 cm³

Base is a right triangle, and the adjacent sides of the right angle (the legs) measure 5 cm and 12 cm

Height of the pyramid: h=?

The formula to calculate the volume of a pyramid is:

`V=(A_(b)h)/(3)`

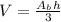
Area of the base: Ab

The base is a right triangle, then to calculate its area we can use the formula to calculate the area of a right triangle:

`A_(b)=(Leg_(1)Leg_(2))/(2)\\ A_(b)=((5 cm)(12 cm))/(2)\\ A_(b)=(60 cm^(2))/(2)\\ A_(b)=30 cm^(2)`

Replacing the known values in the formula of volume:

`80 cm^(3)=((30 cm^(2))h)/(3)\\ 80 cm^(3)=(10 cm^(2) )h`

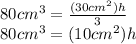
Solving for h: Dividing both sides of the equation by 10 cm²:

`(80 cm^(3))/(10 cm^(2))=((10 cm^(2))h)/(10 cm^(2))\\ 8 cm=h\\ h=8 cm`