Question

Prove Theorem 3: Corresponding angle bisectors of similar triangles are proportional and their ratio is equal to the ratio of similitude.

Answer 1

The proof is given below.

Explanation:

Given the two triangles which are similar we have to prove that the ratio of their angle bisectors and the side or we can say that the ratio of their altitude are proportional.

In ΔABP and ΔDEQ

∠1=∠2 (Given)

∠3=∠4 (each 90°)

By AA similarity rule ΔABP≅ΔDEQ

As if the two triangles are similar then their corresponding sides are proportional

⇒
`(AB)/(DE)=(AP)/(DQ)=(BP)/(EQ)`

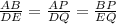
Hence, Corresponding angle bisectors of similar triangles are proportional and their ratio is equal to the ratio of altitude.