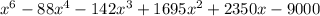Question

Which polynomial function f(x) has a leading coefficient of 1, roots4, 2, and 9 with multiplicity 1, and root-5 with

multiplicity 3?

Answer 1

`x^6-88x^4-142x^3+1695x^2+2350x-9000`

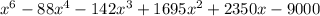
Explanation:

In order to solve this function, we must first start by writting the factors of the polynomial. We can do so by including the given zeros, and the leading coefficient. So we get:

`f(x)=1(x-4)(x-2)(x-9)(x+5)^(3)`

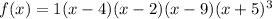
and now we can expand this by multiplying the given parenthesis, so we get:

`f(x)=(x^2-2x-4x+8)(x-9)(x^3+3(5)x^(2)+3(25)x+125)`

`f(x)=(x^2-6x+8)(x-9)(x^3+15x^(2)+75x+125)`

`f(x)=(x^3-9x^2-6x^2+54x+8x-72)(x^3+15x^(2)+75x+125)`

`f(x)=(x^3-15x^2+62x-72)(x^3+15x^(2)+75x+125)`

`f(x)=x^6+15x^5+75x^4+125x^3-15x^5-225x^4-1125x^3-1875x^2+62x^4+930x^3+4650x^2+7750x-72x^3-1080x^2-5400x-9000`

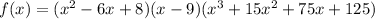
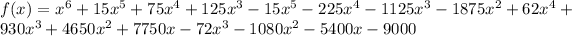
we combine like terms so we get:

`x^6-88x^4-142x^3+1695x^2+2350x-9000`