Question

An isosceles triangle has angle measure 55,55 and 70 the side across from 70 angle is 10 inches long. How long are the other sides

Answer 1

8.72 inches.

Explanation:

Please find the attachment.

Let x be the length of each of equal sides.

We have been given that an isosceles triangle has angle measure 55, 55 and 70 the side across from 70 angle is 10 inches long.

We can see from our attachment that sides across 55 degree angle is x. We will use law of sines to solve for x.

Law of sines represents the relation between the lengths of the sides of a triangle (any shape) to the sines of its angles.

`\frac{a}{\text{sin A}}=\frac{b}{\text{sin B}}=\frac{c}{\text{sin C}}`

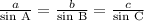
To find the length of x, let us substitute our given values in this equation as:

`\frac{x}{\text{sin(55)}}=\frac{10}{\text{sin(70)}}`

`\frac{x}{\text{sin(55)}}*\text{sin(55)}=\frac{10}{\text{sin(70)}}*\text{sin(55)}`

`x=(10)/(0.939692620786)*0.819152044289`

`x=10.6417777247580839*0.819152044289`

`x=8.7172\approx 8.72`

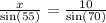
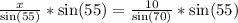
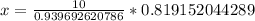
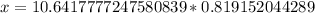
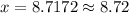
Therefore, the length of other sides is 8.72 inches each.