Answer:
The greatest common factor of given two number can be find by taking common factors and then multiply those factors
 .
.
Explanation:
Given : One number has a prime factorization of
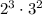 and another number has a prime factorization of
and another number has a prime factorization of
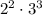 .
.
We have to find an expression that would equal the greatest common factor of these two numbers.
Greatest common factor of numbers is the highest common factor that divides the given numbers.
Prime factorization is the breaking down of a number into primes such that when we take product of those primes we get back the same number.
Given prime factorization of a number as
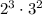
and prime factorization of another number as
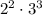 .
.
Here, greatest common factor of given two number can be find by taking common factors and then multiply those factors
 .
.