Question

The speed of a tidal wave in meters/second is given by the square root of the product of the acceleration due to gravity on Earth (9.8 meters/second2) and the depth of the ocean in meters.

If the ocean is 500 meters deep, the speed of the tidal wave will be ____ m/s

Answer 1

70 m/s

Explanation:

"The speed of a tidal wave in meters/second is given by the square root of the product of the acceleration due to gravity on Earth (9.8 meters/second2) and the depth of the ocean in meters":

The sentence above can be interpreted into the equation shown below (letting speed of tidal wave be "s", acceleration due to gravity be "g", and depth be "d"):

`s=√(g*d)`

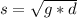
Given d = 500 and g = 9.8, we find speed (s):

`s=√(g*d) \\s=√((9.8)*(500)) \\s=√(4900)\\ s=70`

Hence, the speed is 70 meters per second.