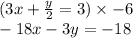Consider this system: 3x + 1/2y = 3 6x - y = 2 Which of the following operations would eliminate the x-terms if the two equations were added together afterward? Multiply the fir…

Question

asked Sep 9, 2020 221k views

2 Answers

Jason Striegel · Answer 1 · 2020-09-11T01:10:28+0000

Answer:

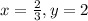
x = (2)/(3), y = 2

Explanation:

We are b:

$3x + (y)/(2) = 3\\6x - y = 2$

We need to eliminate x from the above two equations so that we can find the value of y and then the value of x.

In order to eliminate x we multiply first equation by -2 and add both the equations to solve for y.

This can be shown as:

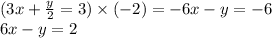
$(3x + (y)/(2) = 3)* (-2) = -6x - y = -6\\6x - y = 2$

Now we add these two equations

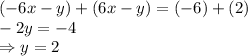
$(-6x - y) + (6x -y) = (-6) + (2)\\-2y = -4\\\Rightarrow y = 2$

Now putting value of y in equation, we get

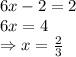
$6x -2 = 2\\6x = 4\\\Rightarrow x = (2)/(3)$

Now, we have to multiply the first equation by -6

$(3x + (y)/(2) = 3)* -6\\ -18x - 3y = -18$

Brennan Casey · Answer 2 · 2020-09-16T14:43:11+0000

Answer:

The correct answer is multiply the first equation by -2.

Explanation:

The reason for this is then you'd be left with the following two equations.

-6x - y = -6

6x - y = 2

If you add these two together you would cancel out the x terms.