Question

How do you create a system of linear equations with an infinite number of solutions using the equation y=2/3x-5

Answer 1

We have the equation,

`y=(2x)/(3)-5`

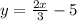
i.e.
`3y=2x-15`

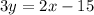
i.e.
`2x-3y=15`

It is required to find a system of equations having infinite solutions.

We know that,

'When the equations are dependent or their graphs are same, the system of equations has infinite number of solutions'.

So, we can take any equation having same graph as that of
`2x-3y=15`.

Let, us take
`4x-6y=30`

So, from the graph of these equations below, we get the system of equations having infinite solutions as,

`2x-3y=15` and
`4x-6y=30`.