Question

James purchased a $205,000 home with a 30-year mortgage at 5.78%. If makes a $1500 monthly mortgage payment, how many months early will he pay off his mortgage? A. 180 months B. 224 months C. 127 months D. 136 months

Answer 1

Answer: 136 months

Explanation:

Answer 2

James will pay off his mortgage 136 months early.

Explanation:

Given : Amount to be paid(A)= $205000

Interest rate per annum = 5.78% = 0.0578

monthly interest rate(i) =
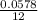`(0.0578)/(12)`= 0.004817 (approx)

Monthly payment (P) = $1500.

we have to find how many months early will he pay off his mortgage

We know,
`P=(A(i))/(1-(1+i)^(-t))`

Substitute values , we get,

`1500=(205000(0.004817))/(1-(1+0.004817)^(-t))`

`1500=(205000(0.004817))/(1-(1.004817)^(-t))`

`1500=(987.416653)/((1-(1.004817)^(-t))`

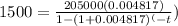
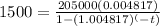
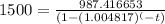
Solving for t ,

`{(1-(1.004817)^t)}=(987.416653)/(1500)\\\\\\{(1-(1.004817)^(-t))}=0.65828\\\\\(1.004817)^(-t)=0.341722`

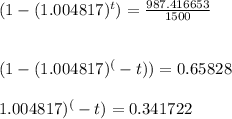
Applying ln both sides,we get,

`\ln \left(1.004817^(-t)\right)=\ln \left(0.341722\right)`

`\mathrm{Apply\:log\:rule}:\quad \log _a\left(x^b\right)=b\cdot \log _a\left(x\right)`

`-t\ln \left(1.004817\right)=\ln \left(0.341722\right)`

`\mathrm{Divide\:both\:sides\:by\:}\ln \left(1.004817\right)`

`(-t\ln \left(1.004817\right))/(\ln \left(1.004817\right))=(\ln \left(0.341722\right))/(\ln \left(1.004817\right))`

`-t=(\ln \left(0.341722\right))/(\ln \left(1.004817\right))`

`t=223.44650\dots`

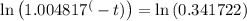
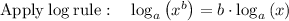
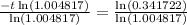
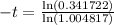
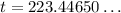
Thus, t = 224 months.

1 year = 12 month thus, 30 years = 360 months.

Difference = 360 - 224 = 136 months

Thus, James will pay off his mortgage (360-224) 136 months early.