Question

Taylor graphs the system below on her graphing calculator and decides that f(x)=g(x) at x=0, x=1, and x=3. Provide Taylor with some feedback that explains which part of her answer is incorrect and why it is incorrect.

f(x)= 2x+1 g(x)= 2x^2+1

Answer 1

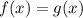`f(x)=g(x)` only at x= 0 and x= 1. They are not equal at x= 3.

Step-by-step explanation:

The functions are given by,
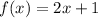`f(x)= 2x+1` and
`g(x)= 2x^2+1`.

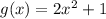We will substitute the values of x. It gives the following table,

`f(x)= 2x+1`
`g(x)= 2x^2+1`

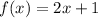
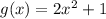
x= 0 f(0)= 2×0+1= 1 g(0)= 2×(0^2)+1= 1

x= 1 f(1)= 2×1+1= 3 g(1)= 2×(1^2)+1= 2+1 = 3

x= 3 f(3)= 2×3+1= 7 g(3)= 2×(3^2)+1= 18+1 = 19

So, from the graphs below and the calculations above, we have,

Hence, the function have equal values only at x= 0 and x= 1.