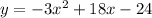Answer:
The standard form as
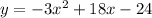
Step-by-step explanation:
Given: A function which is written in vertex form or intercept form.
We have to re-write it in standard form that in terms of

Given
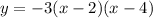
Multiply each term on the right side, we get,
![y =-3[x(x-4)-2(x-4)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/8jyl7e0b0k1a8wbb4c21slq3z7pml4eb4d.png)
![y =-3[x^2-4x-2x+8]](https://img.qammunity.org/2020/formulas/mathematics/high-school/cnii1g3zg1ekoj7wunp34uz60r8i4frhk2.png)
![y =-3[x^2-6x+8]](https://img.qammunity.org/2020/formulas/mathematics/high-school/vb6h4fplo4zfmhvrib2wlrksachduuy2xp.png)
Multiply constant term , we get,
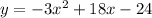
Thus , we have obtained the standard form as