Answer:
Refer below explanation.
Explanation:
Given : two triangles ∆QPK and ∆LMK.
We have to show ∆QPK ≅ ∆LMK.
Two triangles are similar if ratio of the corresponding sides are equal and measure of corresponding angles are equal.
Statement 1)
QK=16, PK=26, MK=65, KL=40 ( Reason: Given)
Statement 2 )

(reason : ratio of corresponding sides)
Statement 3)

Thus,
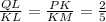
(reason: simplify ratios)
Statement 4)
∠MKL = ∠PQK (reason : Vertically opposite angles)
Statement 5)
∆QPK ≅ ∆LMK (reason : Side-angle-side)
Side angle side similarity criterion states that two angles are similar if the ratio of their corresponding sides and angle between these sides are equal then triangles are similar.