Question

A standard doorway measures 6 feet 8 inches by 3 feet. What is the largest dimension that will fit through the doorway without bending?

Answer 1

87.73 inches

Explanation:

We are given that the dimensions of the rectangular doorway are,

Length = 6 ft 8 inches = 80 inches and Width = 3 feet = 36 inches.

Using Pythagoras Theorem, we will find the diagonal of the rectangular doorway.

i.e.
`hypotenuse^(2)=length^(2)+width^(2)`

i.e.
`hypotenuse^(2)=80^(2)+36^(2)`

i.e.
`hypotenuse^(2)=6400+1296`

i.e.
`hypotenuse^(2)=7696`

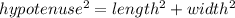
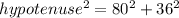
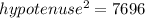
i.e. Hypotenuse = ±87.73 inches

Since, the length cannot be negative.

So, the length of the diagonal is 87.73 inches.

As, the largest side of a rectangle is represented by the diagonal.

So, the largest dimension that will fit through the doorway without bending is 87.73 inches.