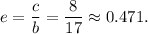Answer:
1. B
2.C
Explanation:
A plot of land in the shape of a vertical ellipse. The equation of the ellipse is
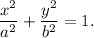
If the foci are 8 feet from the center, then

If the plot of land is 34 feet across the vertical axis, then
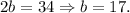
Use formula
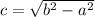 (because ellipse is vertical, then b>a) to find a:
(because ellipse is vertical, then b>a) to find a:
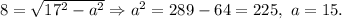
Then the plot of land is 2a=30 ft across the other axis.
If b>a, the eccentricity of the ellipse is