Question

You are designing an amusement park ride with cars that will spin in a circle around a center axis, and the cars are located at the vertices of a regular polygon. The sum of the measures of the angles' vertices is 6120°. If each car holds a maximum of four people, what is the maximum number of people who can be on the ride at one time?

Answer 1

144 people.

Explanation:

Let n be the vertices, where cars are located.

We have been given that the sum of the measures of the angles' vertices is 6120°.

Let us find the number of vertices using formula:

`\text{Sum of all interior angles of a polygon with n sides}=180(n-2)`.

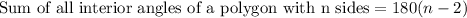Upon substituting the given sum of the measures of the angles in this formula we will get,

`6120=180(n-2)`

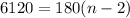
Using distributive property
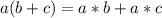`a(b+c)=a*b+a*c` we will get,

`6120=180n-360`

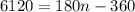
Adding 360 to both sides of our equation we will get,

`6120+360=180n-360+360`

`6480=180n`

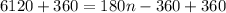
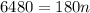
Upon dividing both sides of our equation by 180 we will get,

`(6480)/(180)=(180n)/(180)`

`36=n`

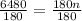
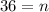
As the cars are located on the vertices of regular polygon, so there will be 36 cars in the ride.

We are told that each car holds a maximum of 4 people, so the number of maximum people who can ride at one time will be equal to 4 times 36.

`\text{Maximum number of people who can be on the ride at one time}=4* 36`

`\text{Maximum number of people who can be on the ride at one time}=144`

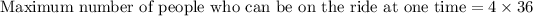
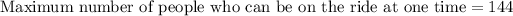
Therefore, the maximum number of people who can be on the ride at one time is 144 people.