Question

What is the value of an investment of $3,500 after 2 years if it earns 1.5% compounded quarterly?

Answer 1

AAAA=3500(1+0.0151)1⋅2=3500⋅1.0152=3500⋅1.030225=3605.79

STEP 2: To find interest we use formula A=P+I, since A=3605.79 and P = 3500 we have:

A3605.79II=P+I=3500+I=3605.79−35

Explanation:

Answer 2

Using formula:

`\text{Amount} = \text{Principal}(1+(r)/(n))^(nt)`

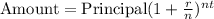
where

P is the principal

r is the annual rate in decimal

n is the number of compounding periods per year

t is the number of years.

As per the statement:

$3,500 after 2 years if it earns 1.5% compounded quarterly.

Here, P = $3500, t= 2 years, r = 1.5% = 0.015 and n = 4

then,

Substitute these values we have;

`\text{Amount} =3500(1+(0.015)/(4))^(2\cdot 4)`

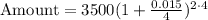
Or

`\text{Amount} =3500(1+0.00375)^(8)`

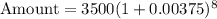
or

`\text{Amount} =3500(1.00375)^(8)`

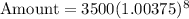
Simplify:

Amount = $3606.38852

Therefore, the value of an investment after 2 years is, $3,606.39