Question

Kim solved the equation below by graphing a system of equations. log base 2 (3x-1) = log base 4 (x+8)

Answer 1

The solution to the given equation is at point (1.353, 1.613). Explanation:

Given : Kim solved the equation below by graphing a system of equations.

`\log_2(3x-1)=\log_4(x+8)`

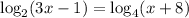
To find : What is the approximate solution to the equation?

Solution :

Let,
`y_1=\log_2(3x-1)`

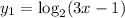
and
`y_2=\log_4(x+8)`

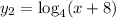
Now, we plot these two equations.

The graph of
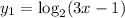`y_1=\log_2(3x-1)` is shown with red line.

The graph of
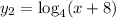`y_2=\log_4(x+8)` is shown with blue line.

The solution to this system will be their intersection point.

The intersection point of these graph is (1.353, 1.613)

Refer the attached graph below.

Therefore, The solution to the given equation is at point (1.353, 1.613).

Answer 2

solution is

`x=1.353,y=1.613`

Explanation:

We are given equation as

`log_2(3x-1)=log_4(x+8)`

Firstly, we will find equations

First equation is

`y=log_2(3x-1)`

Second equation is

`y=log_4(x+8)`

now, we can draw graph

and then we can find intersection point

we can see that

intersection point is (1.353,1.613)

so, solution is

`x=1.353,y=1.613`