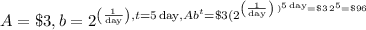Question

You are starting a new job and are told that your pay will be $3 on the first day. Each day after that, your pay will double until you reach the amount of $96. Starting from the first day, on what day will you reach $96?

Answer 1

Answer: day six. A=3, b=2, t=0 to t=5, covering 6 days. $3, $6, $12, $24, $48, $96.

Explanation:

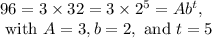`96 = 3*32 = 3*2^5 = Ab^t,\\\text{ with }A=3, b=2,\text{ and }t=5`. A is the starting amount at t=0. b is the base, two because the amount doubles each day. b would be 3 if it tripled every day. t is the final day number, counting from zero.

`A=3,b=2,t=0,Ab^t=3*2^0=3`

`A=3,b=2,t=1,Ab^t=3*2^1=6`

`A=3,b=2,t=2,Ab^t=3*2^2=12`

`A=3,b=2,t=3,Ab^t=3*2^3=24`

`A=3,b=2,t=4,Ab^t=3*2^4=48`

`A=3,b=2,t=5,Ab^t=3*2^0=96`

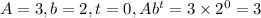
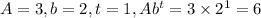
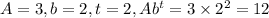
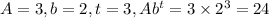
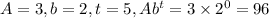
We can also do this with units included.

Obviously the unit for A is dollars, and t is in days. But what is the unit for b?

Well, the amount doubles once _per day_. So try b = 2 per day = 2/day. That doesn't work. The correct value for b including units is

`b=2^\left(\frac{1}{\text{day}}\right)`.

So if you wanted to express time in weeks while still doubling once per day, you would multiply by a value equivalent to one,
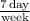`\frac{7\,\text{day}}{\text{week}}`, and cancel units:

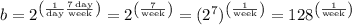`b=2^{\left(\frac{1}{\text{day}}\frac{7\,\text{day}}{\text{week}}\right)}=2^{\left(\frac{7}{\text{week}}\right)}=(2^7)^{\left(\frac{1}{\text{week}}\right)}=128^{\left(\frac{1}{\text{week}}\right)}`.

`A=\$3, b=2^\left(\frac{1}{\text{day}}\right), t=5\,\text{day},\\Ab^t=\$3\big\left(2^\left(\frac{1}{\text{day}}\right)\big\right)^{5\,\text{day}}=\$3\,2^5=\$96`