Question

Match each polynomial with its factorization. 1. y 2 - y - 2 (4y - 3)(y + 2) 2. 3y 2 - 27 3(y - 3)(y + 3) 3. y 4 - 16 -4(y + 2)( y - 4) 4. y 2 - 12y + 36 (y + 1)(y - 2) 5. -4y 2 + 8y + 32 (y - 2)(y + 2)(y2 + 4) 6. 5y - 2 + 4y 2 - 4 (y - 6)2

Answer 1

1. y^2 - y - 2 = (y + 1)(y - 2)

2. 3y^2 - 27 = 3(y - 3)(y + 3)

3. y^4 - 16 = (y - 2)(y + 2)(y^2 + 4)

4. y^2 - 12y + 36 = (y - 6)^2

5. -4y^2 + 8y + 32 = -4(y + 2)( y - 4)

6. 5y - 2 + 4y^2 - 4 = (4y - 3)(y + 2)

Explanation:

1. y^2 - y - 2=(y - 2)(y + 1)→

y^2 - y - 2 = (y + 1)(y - 2)

2. 3y^2 - 27

Common factor 3:

`3y^2-27=3(y^2-9)`

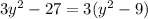
Using Difference of squares:

`a^2-b^2=(a-b)(a+b)`

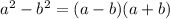
with:

`a^2=y^2\\ √(a^2)=√(y^2)\\ a=y`

`b^2=9\\ √(b^2)=√(9)\\ b=3`

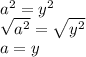
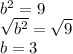
3y^2 - 27=3(y - 3)(y + 3)

3. y^4 - 16

Using Difference of squares:

`a^2-b^2=(a-b)(a+b)`

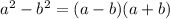
with:

`a^2=y^4\\ √(a^2)=√(y^4)\\ a=y^2`

`b^2=16\\ √(b^2)=√(16)\\ b=4`

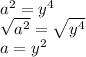
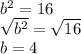
y^4 - 16 = (y^2-4)(y^2+4)

Using Difference of squares in the first parentheses:

`a^2-b^2=(a-b)(a+b)`

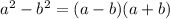
with:

`a^2=y^2\\ √(a^2)=√(y^2)\\ a=y`

`b^2=4\\ √(b^2)=√(4)\\ b=2`

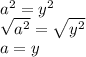
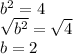
y^4 - 16 = (y - 2)(y + 2)(y^2 + 4)

4. y^2 - 12y + 36 = (y - 6)(y - 6)

y^2 - 12y + 36 = (y - 6)^2

5. -4y^2 + 8y + 32

Common factor -4:

`-4y^2+8y+32=-4(y^2-2y-8)\\ -4y^2+8y+32=-4(y-4)(y+2)`

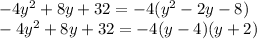
-4y^2 - 12y + 32 = -4(y + 2)( y - 4)

6. 5y - 2 + 4y^2 - 4

Adding like terms:

5y - 2 + 4y^2 - 4 = 5y + 4y^2 - 6

Ordering the terms:

5y - 2 + 4y^2 - 4 = 4y^2 + 5y - 6

Writing 5y like: 8y - 3y = -3y + 8y

5y - 2 + 4y^2 - 4 = 4y^2 - 3y + 8y - 6

Grouping terms:

5y - 2 + 4y^2 - 4 = (4y^2 - 3y) + (8y - 6)

Common factor in the first parentheses y and 2 in the second parentheses:

5y - 2 + 4y^2 - 4 = y(4y - 3) + 2(4y - 3)

Common factor 4y-3:

5y - 2 + 4y^2 - 4 = (4y - 3)(y + 2)