Answer:
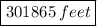
Explanation:
Let the distance be
 and the time be
and the time be
 .
.
It was given that the distance,
 , varies directly as the square of the time
, varies directly as the square of the time
 , we write the proportional relation,
, we write the proportional relation,
 .
.
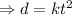 , where
, where
 is the constant of variation.
is the constant of variation.
It was also given that,
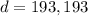 , when
, when
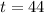 .
.
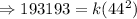
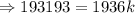
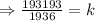
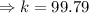
Now the equation of variation becomes;
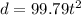
When,
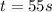 ,
,
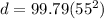
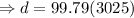
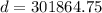
The object will travel 301865 feet in 55 seconds.