Question

According to the Rational Root Theorem, which function has the same set of potential rational roots as the function g(x) = 3x5 – 2x4 + 9x3 – x2 + 12?

Answer 1

The answer is A, or
`f(x) = 3x^(5) - 2x^(4) - 9x^(3) + x^(2) - 12`

If the picture won't load, the correct equation is f(x) = 3x^5 – 2x^4 – 9x^3 + x^2 – 12

Just got it right on the quiz, hope this helps!! :)

Answer 2

Explanation:

Given is an algebraic polynomial of degree 5.

`g(x) = 3x^5-2x^4+9x^3-x^2+12\\`

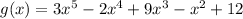
Here leading term is p=3 and constant term is q =12

Factors of p are ±1,±2,±3

Factors of q are
`\frac{±1,±2,±3,±4,±6,±12} \\`

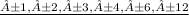
Possible forms of p/q will be the same for any other polynomial of degree 5 with leading term =3 and constant term = 12

Hence any other polynomial

`g(x) = 3x^5+ax^4+bx^3+cx^2+12`

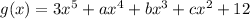
will have same possible zeroes of p/q, when a,b,c are rational.

Hence any polynomial of this type would have the same possible rational roots.