Question

What is the value of x? enter your answer in the box. units triangle a p r with line segment c d parallel to segment a p with c between a and r and d between p and r. a c equals 10. c r equals x. p d equals 15. d r equals 42?

Answer 1

The answer is 28

Explanation:

15 divided by 10 is 1.5,

42 divided by 1.5 equals 28,

hence the answer is 28.

Answer 2

Answer: x = 28 unit

Explanation:

Here, In triangle APR,

CD ║ AP,

Such that, C ∈ AR and D ∈ PR,

Also, AC = 10 unit, CR = x unit, PD = 15 unit and DR = 42 unit,

Since, CD ║ AP,

Thus, by the alternative interior angle theorem,

`\angle APR\cong \angle CDR`

`\angle PAR\cong \angle DCR`

Thus, By AA similarity postulate,

`\triangle APR\sim \triangle CDR`

Since, the corresponding sides of the similar triangle are in same proportion,

`\implies (AR)/(CR)=(PR)/(DR)`

`\implies (AC+CR)/(CR)=(PD+DR)/(DR)`

`\implies (10+x)/(x)=(15+42)/(42)`

`\implies 420 + 42 x = 15 x + 42 x`

`\implies 420 = 57 x - 42 x`

`\implies 420 = 15 x\implies 28 = x`

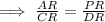
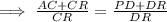
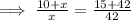
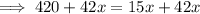
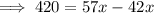
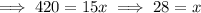
Hence, the value of x = 28.