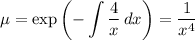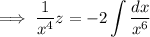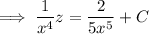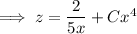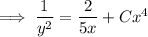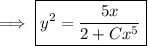(a) This is a Bernoulli equation:
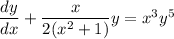
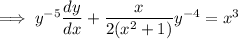
Substitute
 and
and
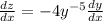 to transform the ODE to
to transform the ODE to
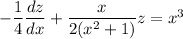

which is now linear in
 . Using the integrating factor method, the I.F. is
. Using the integrating factor method, the I.F. is
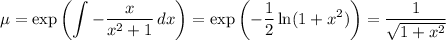
Distribute
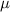 on both sides to get a derivative of a product on the left side.
on both sides to get a derivative of a product on the left side.
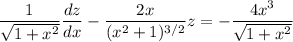
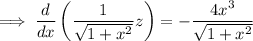
Integrate both sides (the integral on the right can be done by parts) to get
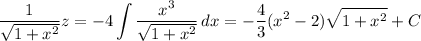
Solve for
 .
.
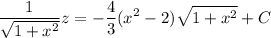
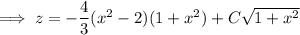
Solve for
 .
.
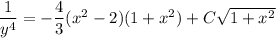
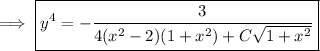
You could go on to solve explicitly for
 if you like.
if you like.
(b) This is also a Bernoulli equation:
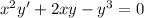

Substitute
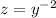 and
and
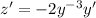 .
.

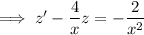
Now repeat the method from (a) to solve for
 .
.