Answer:
Identity is verified.
Explanation:
The given equation is
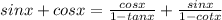
Now to prove this identity we will either convert left hand side of the equation into the right hand side of the equation or the reverse of it.
Now we take right hand side of the identity \frac{cosx}{1-tanx}+\frac{sinx}{1-cotx} and simply solve it.
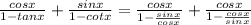
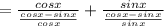
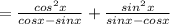
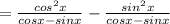
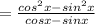
From the formula (a²-b²)=(a+b)(a-b)
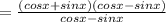
Now we cancel the common terms from numerator and denominator.
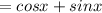 which equal to the left hand side of the equation.
which equal to the left hand side of the equation.
Therefore identity is verified.