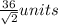Question

The length of a side of a triangle is 36. A line parallel to that side divides the triangle into two parts of equal area. Find the length of the segment determined by the points of intersection between the line and the other two sides of the triangle.

Answer 1

Length of BE is
`(36)/(\sqrt2)units`

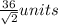
Explanation:

The length of a side of a triangle is 36. A line parallel to that side divides the triangle into two parts of equal area. we have to find the length of the segment determined by the points of intersection between the line and the other two sides of the triangle.

Now, the two parts of triangle have equal area ∴ ar(ADE)=ar(BDEC)

⇒
`ar(ADE)=(1)/(2)ar(ABC)`

⇒
`(ar(ADE))/(ar(ABC))=(1)/(2)`

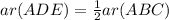
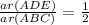
In ΔABE and ΔABC,

∠A=∠A (Common)

∠ABE=∠ABC (Corresponding angles)

By AA similarity, ΔABE is similar to ΔABC.

Hence by area side proportionality theorem

`(ar(ADE))/(ar(ABC))=((BE)/(BC))^2`

⇒
`(1)/(2)=(BE^2)/(36^2)`

⇒
`BE^2=(36^2)/(2)`

⇒
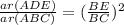
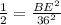
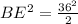
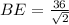`BE=(36)/(\sqrt2)`units

Hence, length of BE is
`(36)/(\sqrt2)units`