Question

for a triangle to be obtuse only one of the angles must br shown to be obtuse. (in fact only one of the angles can possibly be obtuse) but for a triangle to be acute all three angles must be shown to be acute. explain why determining one acute angle with the Pythagorean inequalities theorem shows that the triangle is acute

Answer 1

The explanation is given below.

Explanation:

Given for a triangle to be obtuse only one of the angles must be shown to be obtuse but for a triangle to be acute all three angles must be shown to be acute.

According to Pythagoras theorem for a right angled triangle which has one angle of 90° rest of two are acute.

`a^(2)+b^(2)=c^(2)`

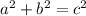
Hence, by Pythagorean inequality

`a^(2)+b^(2)>c^(2)`

which gives the triangle is acute.

Hence, one acute angle with the Pythagorean inequalities theorem shows that the triangle is acute.