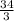Answer:
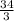
Explanation:
If α + β are the roots of the equation ax² + bx + c = 0 then
(x - α)(x - β) = 0, that is
x² - x(α + β) + αβ = 0
comparing the equation with ax² + bx + c = 0 ( ie. x² +
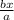 +
+
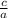 = 0 ) then
= 0 ) then
α + β = -
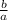 , αβ =
, αβ =
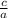
comparing 3x² - 12x + 7 = 0 with ax² + bx + c = 0, gives
a = 3, b = - 12, c = 7, hence
α + β = -
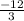 = 4 and αβ =
= 4 and αβ =
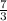
(α + β)² = α² + β² + 2αβ
α² + β² = (α + β)² - 2αβ = 4² -
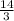 =
=