Answer:
(a)
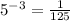
(b)
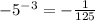
(c)
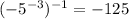
(d)
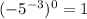
Explanation:
(a)
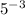
we can use property of exponent
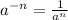
we get
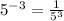
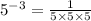
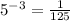 ........Answer
........Answer
(b)
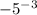
we can use property of exponent
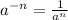
we get
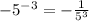
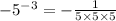
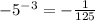 ........Answer
........Answer
(c)
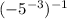
we can use property of exponent
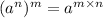
we get
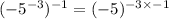
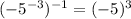
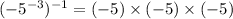
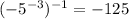 ........Answer
........Answer
(d)
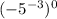
we can use property of exponent
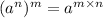
we get
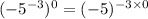
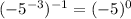
we can use property
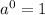
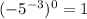 ........Answer
........Answer