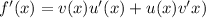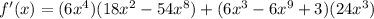Answer:
Q1:
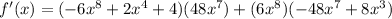
Q2:
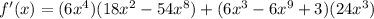
Explanation:
The derivative of the product of two functions is:
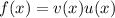
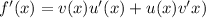
The derivative is the product of the first function and the derivative of the second function added to the product of the second function and the derivative of the first function.
Q1: The function you are given is:
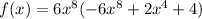
You can think of that function as the product of functions
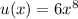 and
and
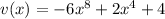
We first find the derivatives of functions u and v:
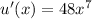 and
and
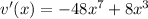
Now we follow the rule above:
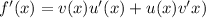
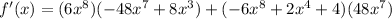
Use the commutative property to change the order of the sum.
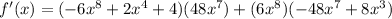
This is the solution you have.
Q2: The function you are given is:
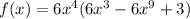
You can think of that function as the product of functions
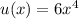 and
and

We first find the derivatives of functions u and v:
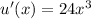 and
and
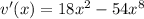
Now we follow the rule above: