Question

The sector of a circle shown to the left has its center at point OO. The arc XYZXYZ has length 10.810.8, and the central angle XOZXOZ has measure 1.81.8 radians. What is the radius length, rr, of the sector?]

Answer 1

6

Explanation:

Correct

Answer 2

Answer: Length of the radius of the sector is 6 units.

Explanation:

Since we have given that

Length of an arc = 10.8

Radian of a central angle = 1.8

First we convert radian into degrees,

`1\ radian= 57.295779513\textdegree\\\\1.8\ radians=1.8*  57.3\textdegree\\\\1.8\ radians=103.14\textdegree`

As we know the formula for "Length of an arc":

`\text{Length of an arc}=(\theta)/(360\textdegree)* 2\pi r\\\\10.8=(103.14)/(360\textdegree)* 2* (22)/(7)* r\\\\10.8=1.8r\\\\r=(10.8)/(1.8)\\\\r=6`

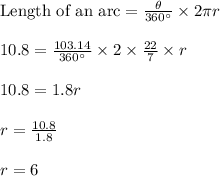
Hence, Length of the radius of the sector is 6 units.