Question

2. The table shows a function. x 0 1 2 3 5 13 21 29 37 45 53 (a) Is the function linear, exponential, or neither? (b) What is the pattern that you observe in the table? (for example: adding 5 each time x increases by 1, dividing by 2 each time x increases by 3) If there is no pattern, show that there is no pattern. (c) What is the y-intercept of the function represented by the table? (be sure to write as an ordered pair)

Answer 1

The Ordered pair of the function is

x : 0 1 2 3 4 5

y: 13 21 29 37 45 53

(a)
`\frac{\text{Change in y values}}{\text{Change in x values}}=(21-13)/(1-0)=(29-21)/(2-1)=(37-29)/(3-2)=(45-37)/(4-3)=(53-45)/(5-4)=8`

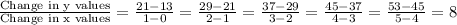
Slope between two points are same.So,the function Represented in terms of ordered pairs Linear.

(b) As, you can each Successor of x values is obtained by adding 1 to it's Predecessor.

and , each Successor of y values is obtained by adding 8 to it's Predecessor.

(c) Taking any two ordered pairs , (0,13) and (1,21) we can find an equation of line passing through these 5 points (2,29),(3,37),(4,45),(5,53)

Equation of line passing through passing through two points
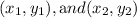`(x_(1),y_(1)),{\text and} (x_(2),y_(2))` is given by

=
`(y-y_(1))/(x-x_(1))=(y_(2)-y_(1))/(x_(2)-x_(1))`

=
`(y-13)/(x-0)=(21-13)/(1-0)`

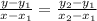
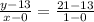
→ y -13 = 8 x

→ y = 8 x + 13

So, Y intercept = 13