Question

PLEASE HELP IM SOOOOOO CONFUSED!

Given: BC/CD = AC/CE

Prove: △ACD ~ △ECD


Statement: Reason:

BC/CD = AC/CE ?

? ?

? ?


Answer Choice:

△ACB ~ △ECD

Vertical ∠'s

SAS

Given

△BCA = △ECD

Answer 1

Hello,

Statement: Reasons:

1. BC/CD = AC/CE 1. Given
2. ∠BCA = ∠ECD 2. Vertical ∠'s =
3. △ACB ~ △ECD 3. SAS

Hope it helps!

Answer 2

Given:

`(BC)/(CD)=(AC)/(CE)`

Prove:

`\triangle ACD \sim \triangle ECD`

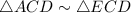
To prove a similarity we can recur to different postulates which we can defined below.

Angle-Angle postulate (AA): if two triangles have two of their angles congruent, then those angles are similar.

Side-Angle-Side postulate (SAS): if two triangles have to pair of sides proportional (in the same ratio), and the included pair of angles are congruent, then those triangles are similar.

Side-Side-Side postulate (SSS): if two triangles have all three pairs of sides in the same ration, then those triangles are similar.

Basically, we can proof that sides are proportional or that their angles are congruent, either way will give us the proof.

1.
`(BC)/(CD)=(AC)/(CE)`, by given.

2.
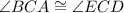`\angle BCA \cong \angle ECD`, by vertical angles definiton.

3.
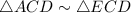`\triangle ACD \sim \triangle ECD`, by SAS postulate.

You can observe that we used SAS postulate, because by given we already had two proportional pair of sides.