Question

Could someone help me to solve this que?

Answer 1

The speed of the ball B is 6.4 m/s. The direction is 50 degrees counterclockwise.

Step-by-step explanation:

Assuming the collision is elastic, use the conservation of momentum to solve this problem. The conservation law implies that:

`m\vec v_(A0)+m\vec v_(B0) = m\vec v_(A1)+m\vec v_(B1)`

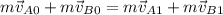
(the total momentum of the two balls is the same before (index 0) and after (index 1) the collision). Since B is stationary and A and B have the same mass, this simplifies to:

`\vec v_(A0) = \vec v_(A1)+\vec v_(B1)`

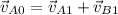
and allows us to determine the velocity of ball B after the collision:

`\vec v_(B1) = \vec v_(A0)-\vec v_(A1)`

The above involves vectors. Your problem suggests to use the component method, which I am assuming means solving the above equation separately along the x and y axes. Define x to align with the original line of motion of the ball A before the collision, and y to be perpendicular to x, pointing up:

`v_(B1x) = v_(A0x)-v_(A1x)\\v_(B1y) = v_(A0y)-v_(A1y)`

We just need to compute the x- and y-components of the known velocity of the ball A. Drs. Sine and Cosine come to help here.

`v_(A1x) = |v_(A1)|\cos 40^\circ\\v_(A1y) = |v_(A1)|\sin 40^\circ`

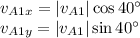
so

`v_(B1x) = |v_(A0)|\cos 0^\circ-|v_(A1)|\cos 40^\circ=(10.0-7.7\cdot 0.77) (m)/(s)\approx 4.1(m)/(s)\\v_(B1y) = |v_(A0)|\sin 0^\circ-|v_(A1)|\sin 40^\circ=(0-7.7\cdot 0.64) (m)/(s)\approx -4.9(m)/(s)`

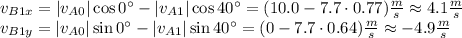
The speed of the ball B is
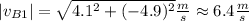`|v_(B1)| = √(4.1^2+(-4.9)^2)(m)/(s)\approx 6.4 (m)/(s)`. The direction (angle from horizontal) is
`\beta = \arcsin (-(4.9)/(6.4))\approx -50^\circ`, i.e., 50 degrees counterclockwise.