Question

1) Consider the given inequality and its solution. In which step, if any, is there an error?

A) Step 1
B) Step 2
C) Step 3
D) There is no error in the solution.

2) Which is the correct solution?
A) x ≤ 3
B) x ≥ −3
C) x ≤ -1/3
D) x ≥ −1/3

Answer 1

The error is in STEP 3.
In any type of inequality one is not allowed to transpose(multiply or divide) any negative number. We can only divide it by positive numbers. if we multiply it by a negative real number the inequality reverses.
for example:

`- x + 1 \geqslant 0 \\ - x \geqslant - 1 \\ (multiplying \: both \: sides \: by \: - 1) \\ x \leqslant 1`

Answer 2

Part (A) The wrong step is step 3

Part (B) The correct option is D) x ≥ −1/3

Explanation:

Consider the provided inequality.

`4-6x\geq -15x+1`

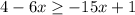
Step 1. subtract 1 from both the sides.

`4-1-6x\geq -15x+1-1`

`3-6x\geq -15x`

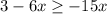
Step 2. Add 6x both sides.

`3-6x+6x\geq -15x+6x`

`3\geq -9x`

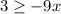
Step 3. Divide both sides by -9 and change the sign of inequality.

`(3)/(-9)\leq (-9x)/(-9)`

`(-1)/(3)\leq x`

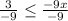
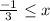
Part (A) The wrong step is step 3

Part (B)

From the above calculation the solution of the inequality is
`(-1)/(3)\leq x`

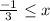
Hence, the correct option is D) x ≥ −1/3