Question

A circle is inscribed in a rhombus with sides of length 4cm. If the two acute angles in the rhombus each measure 60 degrees, what is the length of the circle's radius? Express your answer in simplest radical form.

Answer 1

Explanation:

Given a circle is inscribed in a rhombus with sides of length 4 cm. If the two acute angles in the rhombus each measure 60 degrees. we have to find the radius of circle.

In the rhombus the acute angles is of 30° and also the line OE is perpendicular to side AB and also bisects the side AB gives AE= 2 cm

In ΔAOE , ∠OAE=30°

AE= 2 cm

⇒
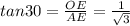
`tan30=(OE)/(AE)=(1)/(√(3))`

⇒
`OE= (2)/(√(3))=(2)/(3)√(3)`