Question

Drag each tile to the correct box. Arrange the angles in increasing order of their cosines.

3(pi)/4
(pi)
7(pi)/6
5(pi)/3
7(pi)/4
4(pi)/3
3(pi)/2
2(pi)

Answer 1

`(3\pi)/(4) <\pi <(7\pi)/(6)<(4\pi)/(3)<(3\pi)/(2)<(5\pi)/(3)<(7\pi)/(4)<2\pi`

Explanation:

we are given different angles

we can see that each angles have different denominators

so, firstly we will find common denominators

denominators are 1 , 2,3,4,6

so, LCD will be 12

now, we will make denominator of all terms 12

`(3\pi)/(4) =(3\pi* 3)/(4* 3)=(9\pi)/(12)`

`\pi =(\pi* 12)/(1* 12)=(12\pi)/(12)`

`(7\pi)/(6) =(7\pi* 2)/(6* 2)=(14\pi)/(12)`

`(5\pi)/(3) =(5\pi* 4)/(3* 4)=(20\pi)/(12)`

`(7\pi)/(4) =(7\pi* 3)/(4* 3)=(21\pi)/(12)`

`(4\pi)/(3) =(4\pi* 4)/(3* 4)=(16\pi)/(12)`

`(3\pi)/(2) =(3\pi* 6)/(2* 6)=(18\pi)/(12)`

`2\pi =(2\pi* 12)/(1* 12)=(24\pi)/(12)`

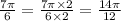
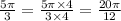
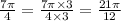
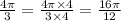
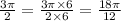
we can see that denominators are same

so, we can arrange it according to numerators as

`(9\pi)/(12) <(12\pi)/(12)<(14\pi)/(12)<(16\pi)/(12)<(18\pi)/(12)<(20\pi)/(12)<(21\pi)/(12)<(24\pi)/(12)`

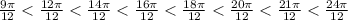
we can replace values

and we get order as

`(3\pi)/(4) <\pi <(7\pi)/(6)<(4\pi)/(3)<(3\pi)/(2)<(5\pi)/(3)<(7\pi)/(4)<2\pi`