Question

Select all that apply. Solve for x , 0 < x < 360;

cos 2x + cos^2 x = 1


answer choices


35

145

215

325

Answer 1

All options are correct

Explanation:

1. Note that

`\cos 2x=2\cos ^2x-1.`

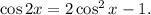
2. Substitute previous expression into the equation:

`2\cos ^2x-1+\cos^2x=1,\\ \\3\cos^2x=2,\\ \\\cos^2x=(2)/(3),\\ \\\cos x=\pm\sqrt{(2)/(3)}.`

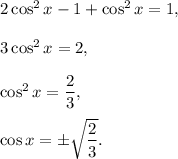
3. If 0° < x < 360°, then

`x=\arccos \left(\sqrt{(2)/(3)}\right)\approx 35^(\circ);`;

`x=180^(\circ)-35^(\circ)=145^(\circ);`

`x=180^(\circ)+35^(\circ)=215^(\circ);`

`x=360^(\circ)-35^(\circ)=325^(\circ).`

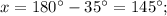
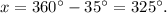
All options are true.

Or you can solve this equation graphically. Plot the graph of the function
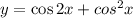`y=\cos2x+cos^2x` that represents the left side of the equation and the graph of the function
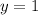`y=1` that represents the right side of the equation. their common points are solutions.