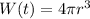Question

Water is poured into the top half of a spherical tank at a constant rate. If W(t) is the rate of increase of the depth of the water, then W is:

Answer 1

Answer with explanation:

Let V be the volume of the tank.

Water is being poured into the spherical tank at a constant rate.

Let r, be the radius of spherical tank.

`(dr)/(dt)=\text{Constant}=r`

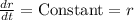
As, radius is constant. --------------------------------(1)

Volume of tank will increase with time.

So,⇒ Height of sphere=Radius of sphere

Volume of Spherical tank

`V=(4\pi r^3)/(3)\\\\(dv)/(dt)=4\pi r^2(dr)/(dt)\\\\=4\pi r^2* r`

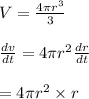
-----------------[using (1)]

So,

`W(t)=4\pi r^3`